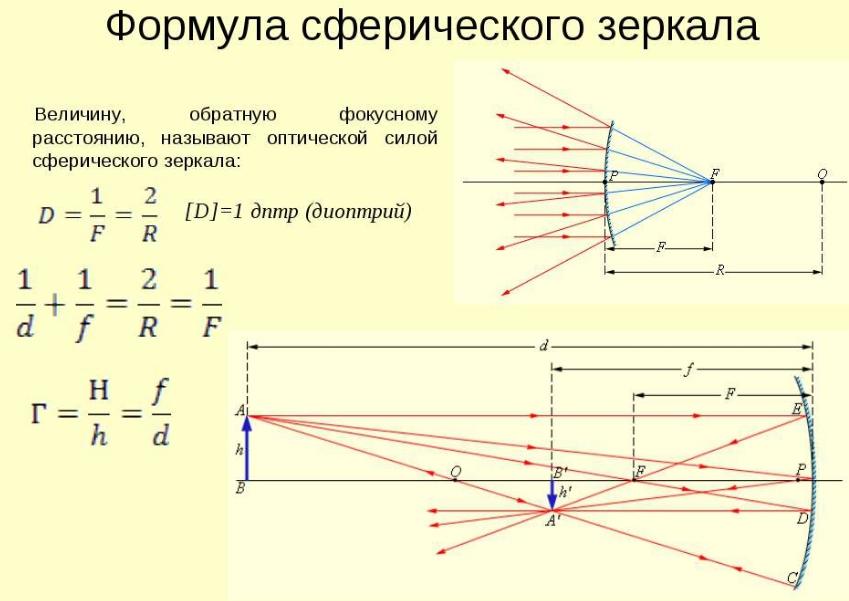
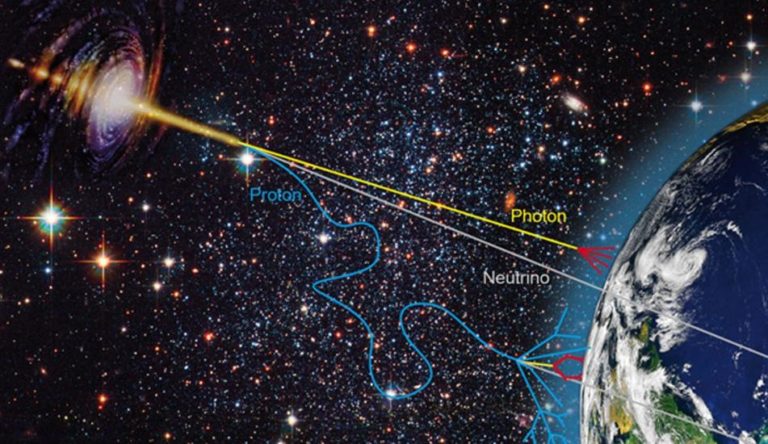
Valon heijastuksen lait ja niiden löytämisen historia

Valon heijastuksen laki löydettiin havaintojen ja kokeiden avulla. Tietysti se voidaan johtaa teoreettisesti, mutta kaikki nyt käytetyt periaatteet on määritelty ja perusteltu käytännössä. Tämän ilmiön pääpiirteiden tunteminen auttaa valaistuksen suunnittelussa ja laitteiden valinnassa. Tämä periaate toimii myös muilla alueilla - radioaalloissa, röntgensäteissä jne. käyttäytyä heijastuksessa täsmälleen samoin.

Mikä on valon heijastus ja sen lajikkeet, mekanismi

Laki on muotoiltu seuraavasti: tuleva ja heijastuneet säteet sijaitsevat samassa tasossa, ja niillä on kohtisuorassa tulopisteestä tulevaan heijastavaan pintaan nähden. Tulokulma on yhtä suuri kuin heijastuskulma.

Pohjimmiltaan heijastus on fysikaalinen prosessi, jossa säde, hiukkaset tai säteily ovat vuorovaikutuksessa tason kanssa. Aaltojen suunta muuttuu kahden väliaineen rajalla, koska niillä on erilaiset ominaisuudet.Heijastunut valo palaa aina siihen väliaineeseen, josta se tuli. Useimmiten heijastuksen aikana havaitaan myös aaltojen taittuminen.

Tämä on kaavamainen selitys valon heijastuksen laista.

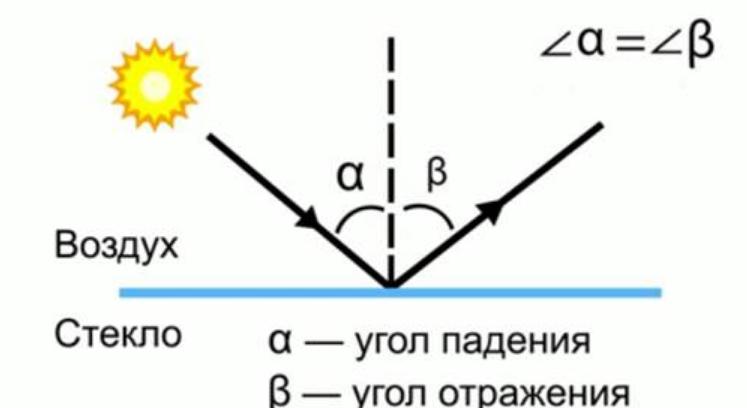
Peilin heijastus

Tässä tapauksessa heijastuneiden ja tulevien säteiden välillä on selvä suhde, tämä on tämän lajikkeen pääominaisuus. Peilauksessa on useita pääkohtia:

1. Heijastunut säde on aina tasossa, joka kulkee tulevan säteen ja heijastavan pinnan normaalin läpi, joka rekonstruoidaan tulokohdassa.
2. Tulokulma on yhtä suuri kuin valonsäteen heijastuskulma.
3. Heijastuneen säteen ominaisuudet ovat verrannollisia säteen polarisaatioon ja sen tulokulmaan. Indikaattoriin vaikuttavat myös näiden kahden ympäristön ominaisuudet.

Peilausheijastuksessa tulo- ja heijastuskulmat ovat aina samat.

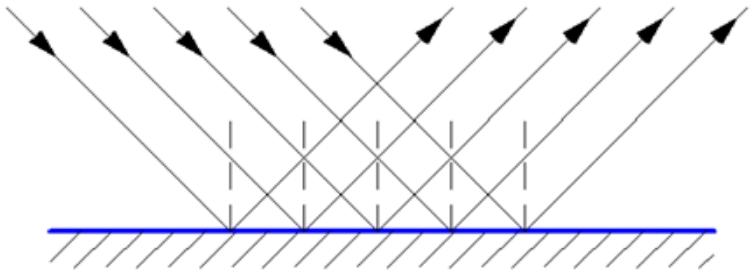
Tässä tapauksessa taitekertoimet riippuvat tason ominaisuuksista ja valon ominaisuuksista. Tämä heijastus löytyy kaikkialta, missä on sileitä pintoja. Mutta eri ympäristöissä olosuhteet ja periaatteet voivat muuttua.

Täydellinen sisäinen heijastus

Tyypillinen äänelle ja sähkömagneettisille aalloille. Tapahtuu kohdassa, jossa kaksi ympäristöä kohtaavat. Tässä tapauksessa aaltojen tulee pudota väliaineesta, jossa etenemisnopeus on pienempi. Valon suhteen voidaan sanoa, että taitekertoimet kasvavat tässä tapauksessa suuresti.

Sisäinen kokonaisheijastus on ominaista veden pinnalle.

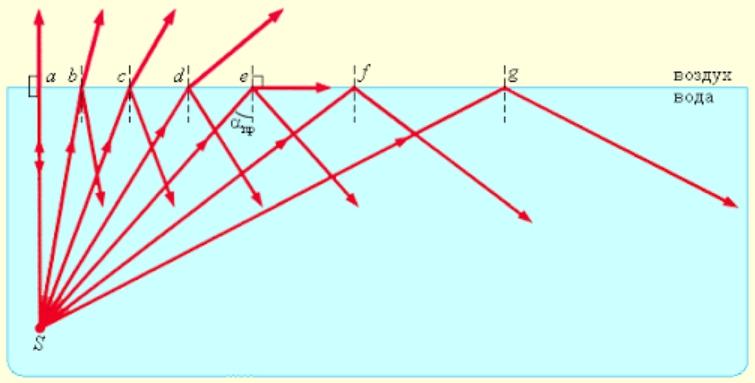
Valosäteen tulokulma vaikuttaa taitekulmaan. Sen arvon kasvaessa heijastuneiden säteiden intensiteetti kasvaa ja taittuneiden säteiden intensiteetti vähenee.Kun tietty kriittinen arvo saavutetaan, taitekertoimet laskevat nollaan, mikä johtaa säteiden kokonaisheijastukseen.

Kriittinen kulma lasketaan erikseen eri väliaineille.

Valon hajaheijastus

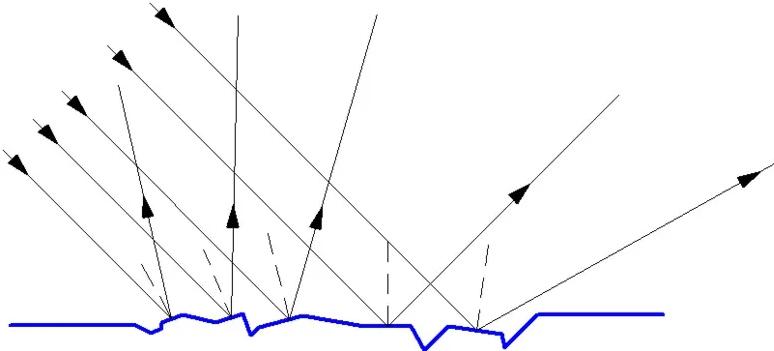
Tälle vaihtoehdolle on ominaista se, että kun se osuu epätasaiseen pintaan, säteet heijastuvat eri suuntiin. Heijastunut valo yksinkertaisesti hajoaa ja tämän vuoksi et näe heijastustasi epätasaisella tai mattapinnalla. Säteen diffuusioilmiö havaitaan, kun epäsäännöllisyydet ovat yhtä suuria tai suurempia kuin aallonpituus.

Tässä tapauksessa yksi ja sama taso voi heijastaa diffuusisti valoa tai ultraviolettia, mutta samalla heijastaa infrapunaspektriä hyvin. Kaikki riippuu aaltojen ominaisuuksista ja pinnan ominaisuuksista.

Diffuusi heijastus on kaoottista johtuen pinnan epätasaisuuksista.

Käänteinen heijastus

Tämä ilmiö havaitaan, kun säteet, aallot tai muut hiukkaset heijastuvat takaisin eli kohti lähdettä. Tätä kiinteistöä voidaan käyttää tähtitieteessä, luonnontieteissä, lääketieteessä, valokuvauksessa ja muilla aloilla. Teleskooppien kuperalinssijärjestelmän ansiosta on mahdollista nähdä sellaisten tähtien valo, jotka eivät näy paljaalla silmällä.

Takaheijastusta voidaan ohjata heijastavan pinnan pallomaisella muodolla.

On tärkeää luoda tietyt olosuhteet valon palaamiselle lähteeseen, tämä saavutetaan useimmiten optiikan ja säteiden säteen suunnan avulla. Tätä periaatetta käytetään esimerkiksi ultraäänitutkimuksissa, koska heijastuneiden ultraääniaaltojen ansiosta kuva tutkittavasta elimestä näkyy monitorissa.

Heijastuksen lakien löytämisen historia

Tämä ilmiö on ollut tiedossa jo pitkään.Ensimmäistä kertaa valon heijastus mainittiin teoksessa "Katoptrik", joka juontaa juurensa 200 eKr. ja sen on kirjoittanut antiikin kreikkalainen tutkija Euclid. Ensimmäiset kokeet olivat yksinkertaisia, joten teoreettista perustaa ei tuolloin ilmestynyt, mutta hän löysi tämän ilmiön. Tässä tapauksessa käytettiin Fermatin peilipintojen periaatetta.

Lue myös

Kuinka nopeasti valo etenee tyhjiössä

 

Fresnel-kaavat

Auguste Fresnel oli ranskalainen fyysikko, joka kehitti useita kaavoja, joita käytetään laajalti tähän päivään asti. Niitä käytetään heijastuneiden ja taittuneiden sähkömagneettisten aaltojen intensiteetin ja amplitudin laskemiseen. Samanaikaisesti niiden on läpäistävä selkeä raja kahden eri taitearvon omaavan väliaineen välillä.

Kaikkia ilmiöitä, jotka sopivat ranskalaisen fyysikon kaavoihin, kutsutaan Fresnel-heijastukseksi. Mutta on muistettava, että kaikki johdetut lait ovat päteviä vain silloin, kun mediat ovat isotrooppisia ja niiden välinen raja on selvä. Tässä tapauksessa tulokulma on aina yhtä suuri kuin heijastuskulma, ja taittumisen arvo määräytyy Snellin lain mukaan.

On tärkeää, että kun valo putoaa tasaiselle pinnalle, polarisaatiota voi olla kahdenlaisia:

1. p-polarisaatiolle on tunnusomaista se, että sähkömagneettisen kentän vektori on tulotasossa.
2. s-polarisaatio eroaa ensimmäisestä tyypistä siinä, että sähkömagneettisen aallon intensiteettivektori sijaitsee kohtisuorassa sitä tasoa vastaan, jossa sekä tuleva että heijastuva säde sijaitsevat.

Fresnel päätteli koko joukon kaavoja, joiden avulla voit suorittaa kaikki tarvittavat laskelmat.

Eri polarisaatioiden tilanteiden kaavat vaihtelevat.Tämä johtuu siitä, että polarisaatio vaikuttaa säteen ominaisuuksiin ja se heijastuu eri tavoin. Kun valo putoaa tietyssä kulmassa, heijastuva säde voi olla täysin polarisoitunut. Tätä kulmaa kutsutaan Brewster-kulmaksi, se riippuu väliaineen taiteominaisuuksista rajapinnassa.

Muuten! Heijastunut säde on aina polarisoitunut, vaikka tuleva valo olisi polarisoimaton.

Huygensin periaate

Huygens on hollantilainen fyysikko, joka onnistui johtamaan periaatteet, jotka mahdollistavat minkä tahansa luonteen aaltojen kuvaamisen. Sen avulla he useimmiten todistavat sekä heijastuslain että valon taittumisen laki.

Tämä on Huygensin periaatteen yksinkertaisin kaavamainen esitys.

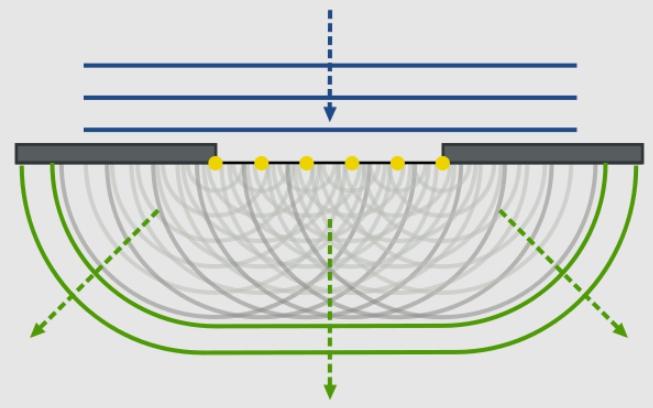
Tässä tapauksessa valo ymmärretään litteäksi aalloksi, eli kaikki aaltopinnat ovat tasaisia. Tässä tapauksessa aallon pinta on joukko pisteitä, joilla on samassa vaiheessa värähtelyjä.

Sanamuoto menee näin: mistä tahansa pisteestä, johon häiriö on tullut, tulee myöhemmin pallomaisten aaltojen lähde.

Videolla 8. luokan fysiikan laki selitetään hyvin yksinkertaisin sanoin käyttämällä grafiikkaa ja animaatiota.

Fedorovin vuoro

Sitä kutsutaan myös Fedorov-Ember-ilmiöksi. Tässä tapauksessa tapahtuu valonsäteen siirtymä ja täydellinen sisäinen heijastus. Tässä tapauksessa siirtymä on merkityksetön, se on aina pienempi kuin aallonpituus. Tämän siirtymän vuoksi heijastunut säde ei ole samassa tasossa tulevan säteen kanssa, mikä on vastoin valon heijastuksen lakia.

Tieteellisen löydön diplomin sai F.I. Fedorov vuonna 1980.

Neuvostoliiton tiedemies todisti teoriassa säteiden sivuttaissiirtymän vuonna 1955 matemaattisten laskelmien ansiosta. Mitä tulee tämän vaikutuksen kokeelliseen vahvistukseen, ranskalainen fyysikko Amber teki sen hieman myöhemmin.

Lain käyttö käytännössä

Esimerkkejä valon heijastumisesta on kaikkialla.

Kyseinen laki on paljon yleisempi kuin miltä näyttää. Tätä periaatetta käytetään laajasti eri aloilla:

1. Peili on yksinkertaisin esimerkki. Se on sileä pinta, joka heijastaa hyvin valoa ja muun tyyppistä säteilyä. Käytössä on sekä litteitä versioita että muun muotoisia elementtejä, esimerkiksi pallomaiset pinnat mahdollistavat esineiden siirtämisen pois, mikä tekee niistä välttämättömiä auton taustapeileinä.
2. Erilaisia ​​optisia laitteita toimii myös harkittujen periaatteiden ansiosta. Tämä sisältää kaiken aina laseista, joita löytyy kaikkialta, tehokkaisiin kaukoputkiin kuperilla linsseillä tai lääketieteessä ja biologiassa käytettyihin mikroskooppeihin.
3. Ultraäänilaitteet käyttää myös samaa periaatetta. Ultraäänilaitteisto mahdollistaa tarkat tutkimukset. Röntgensäteet etenevät samojen periaatteiden mukaan.
4. mikroaaltouunit - Toinen esimerkki kyseessä olevan lain soveltamisesta käytännössä. Se sisältää myös kaikki infrapunasäteilyllä toimivat laitteet (esimerkiksi pimeänäkölaitteet).
5. koverat peilit antaa taskulamppujen ja lamppujen parantaa suorituskykyä. Tässä tapauksessa hehkulampun teho voi olla paljon pienempi kuin ilman peilielementin käyttöä.

Muuten! Valon heijastuksen kautta näemme kuun ja tähdet.

Valon heijastuslaki selittää monia luonnonilmiöitä, ja sen ominaisuuksien tuntemus mahdollisti nykyaikanamme laajalti käytettyjen laitteiden luomisen.